Para hablar de álgebra de Boole es necesario retomar primero la historia del álgebra, la cual tuvo su inicio en el antiguo Egipto y Babilonia, donde resolvieron ecuaciones lineales y cuadráticas, e igualmente ecuaciones indeterminadas con varias incógnitas.
Esta vieja sabiduría acerca de resolución de ecuaciones fue acogida en el mundo islámico, en donde se nombró como “ciencia de reducción y equilibrio”.
A finales del siglo IX, Abu Kamil un matemático egipcio, nombró y demostró las leyes fundamentales e identidades del álgebra.
En la edad media, los matemáticos árabes fueron capaces de representar cualquier potencia de la incógnita “x”, y desarrollaron el álgebra fundamental de los polinomios.
En el siglo XVI hubo un avance importante en el álgebra, el cual fue la introducción de símbolos para las incógnitas, las operaciones y potencias algebraicas.
Después del descubrimiento de Hamilton (las cuaternas 1), el matemático alemán Hermann Grassmann empezó a investigar los vectores, lo que llevó a George Boole a escribir Investigación sobre las leyes del pensamiento en 1854, un tratamiento algebraico de la lógica básica. Desde entonces, el álgebra moderna o álgebra abstracta ha seguido evolucionando hasta descubrir aplicaciones en las otras ciencias2.
El Algebra Booleana es una de los temas que han sido de gran utilidad para los programadores, los físicos entre otras personas que emplean este contenido para dar solución a dificultades presentadas, por ende el señor George Boole fue buen matemático en el cual se basa en el sistema binario uno de los sistemas mas antiguos a través de la historia, igualmente, dio pie para que se empleara en otros campos de acción.
El matemático y filosofo George Boole manejo uno de los sistemas de numeración posicional mas complicados de emplear, ya que solo utilizar el uno (1) y el cero (0), no emplea los demás dígitos, sin embargo lo empleo perfectamente, no obstante por utilizar este sistema de numeración posicional, si no también empleando el tema de los conjuntos como; unión, intersección y complemento3
El tema de los conjuntos se emplean también en muchos otros temas pero para el sistema de numeración binario el método empleado con estos fue tan eficaz ya que para el conjunto de la unión se emplea en las proposiciones complejas como el conector lógico de la “disyunción”, y para la multiplicación se emplea en las proposiciones complejas como el conector lógico de la “conjugación”, se hace referencia a estos dos tipos de conectores lógicos con las operaciones de la suma y de la multiplicación, ya que en esta algebra solo se requiere estas dos operaciones y estos dos conjuntos.
Entrando al tema de el algebra de Booleana ya se ha identificado las operaciones empleadas pero también toca dar alusión a que este matemático realizo la unión de la lógica preposicional con el tema tratado4, ya que valores de verdad como falso o verdadero, si o no, apagado y/o encendido, en el Algebra Booleana se emplean el 1 para el valor de verdad de “falso” y el 0 (cero) para el valor de verdad de “verdadero” 5
De esta forma es mas fácil manejar la tabla de verdad, en la cual el Algebra de Boole lo requiere, sin embargo cave comentar que las palabras “AND”, “OR”, “NOR”, son empleadas en las operaciones de la suma (OR), en la multiplicación (AND), y en el complemento (NOR), sin embargo estas palabras son más empleadas en programación.
No obstante luego de darse a conocer esta algebra, fue de gran utilidad para la programación, ya que muchos de los programas emplean esto, inclusive los circuitos son empleados en los interruptores y en la física para la investigación y utilización de los condensadores.8
Para el desarrollo del álgebra de Boole es importante tener en cuenta las siguientes propiedades:
♦Idempotente respecto a la primera función: x + x = x.
♦Idempotente respecto a la segunda función: xx = x.
♦Maximalidad del 1: x+1=1.
♦Minimalidad del 0: x0 = 0.
♦Involución: x'' = x.
♦Inmersión respecto a la primera función: x + (xy) = x.
♦Inmersión respecto a la segunda función: x(x + y) = x.
♦Ley de Morgan respecto a la primera función: (x + y)' = x’y’.
♦Ley de Morgan respecto a la segunda función: (xy)' = x' + y'
(Nota: en las anteriores propiedades se toma la negación como una comilla sencilla (’))
Cabe resaltar además quien fue George Boole, él nació el 2 de noviembre de 1815 y murió el 8 de diciembre de 1864, fue un matemático y filósofo británico que inventó el álgebra de Boole que es la base de la aritmética computacional moderna. “En 1854 publicó "An Investigation of the Laws of Thought" en él desarrollaba un sistema de reglas que le permitía expresar, manipular y simplificar, problemas lógicos y filosóficos cuyos argumentos admiten dos estados (verdadero o falso) por procedimientos matemáticos.”9
Finalmente el invento del álgebra de Boole fue un avance importante para la ciencia moderna que se desprendió del álgebra en general, dándonos la enseñanza que tanto en la matemática, como en la ciencia, como en la vida cotidiana, deben y existen solo dos respuestas lógicas (verdadero o falso), que nos llevaran a tomar decisiones buenas o malas según sea el caso.
EJERCICIO
Sea el caso:
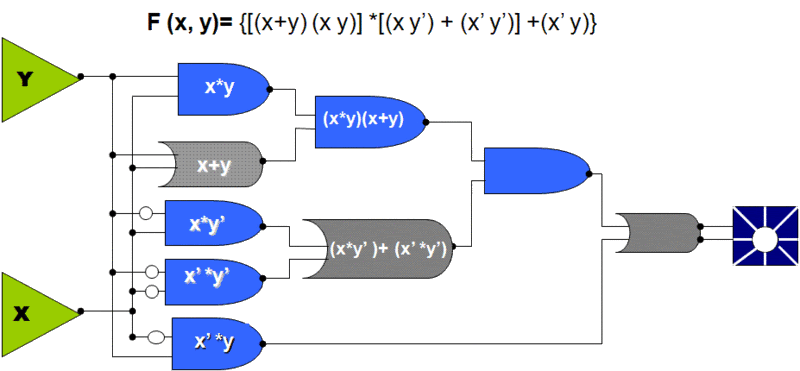
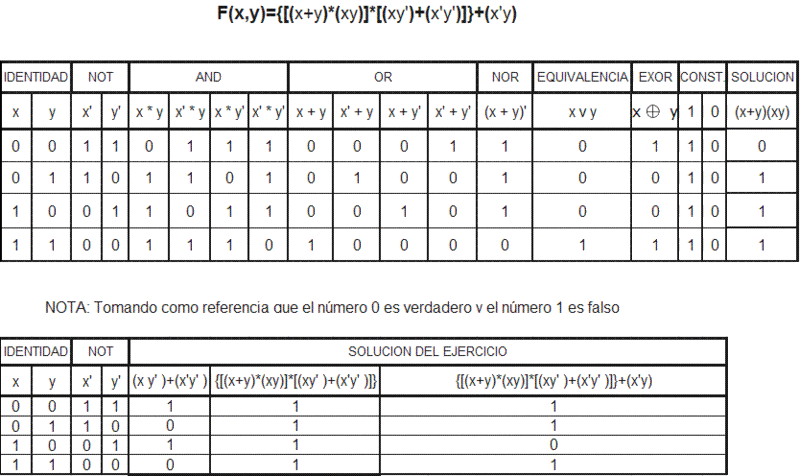
F: (x, y)= {[(x+y) (x y)] *[(x y’) + (x’ y’)] (x’ y)}
DIAGRAMA:
CITAS:
-Las cuaternas fueron descubiertas por el matemático y astrónomo irlandés William Rowan Hamilton, quien desarrolló la aritmética de los números complejos para las cuaternas; mientras que los números complejos son de la forma a+b, las cuaternas son de la forma a + b +c +d. véase 1
-http://www.scribd.com/doc/4123705/Breve-historia-del-Algebrahistoria-del-Algebra Vease 2
-tomado el 29 de Mayo del 2009 http://es.wikipedia.org/wiki/Algebra_booleanakipedia.org/wiki/Algebra_booleana Vease3
-tomado el 29 de Mayo del 2009 http://www.monografias.com/trabajos14/algebra-booleana/algebra-booleana.shtml véase 4
-tomado del libro Matemática digital. Véase 5
-tomado del libro de matemática digital. Véase 6
-sacado el 29 de mayo del 2009 http://es.wikipedia.org/wiki/Diagrama_de_Veitch véase 7
-tomado el 29 de mayo del 2009 http://www.monografias.com/trabajos14/algebra-booleana/algebra-booleana.shtml Véase 8
-http://es.wikipedia.org/wiki/Boole Vease 9
-http://algebraboolelogica.blogspot.com/
-Anexamos que todo lo tomado se encuentra en la webpage; http://www.algebrabooleana.tk/

No hay comentarios:
Publicar un comentario